These are tensors of type 0/1 and they map four- vectors into
the reals. They are denoted by 
, so
is a real
number. One- forms form a vector
space since
It is called the dual vector space to distinguish it from the space of
four- vectors.
The components of are
.
We can write
Generally we have
Note that the signs are positive [ c.f
].
We can think of vectors as columns and one- forms as rows:
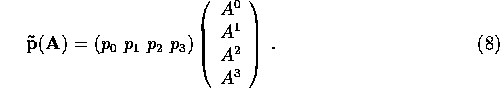
is more fundamental than 
since the latter is defined only if there is a metric i.e. 
.
Now let us look at how one- forms transform :
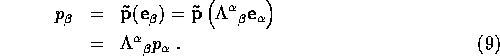
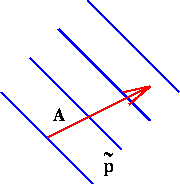
Figure 3.1: 
is the number of surfaces the vector 
pierces.
So one- forms transform like basis vectors, not like vector components.
Now since
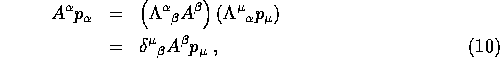
we have
so is frame independent.
We can introduce a one- form basis
, so that
Then
so we must have
This gives the basis for one- forms. It is said to be dual to
.
One can show that
so the basis one- forms transform like vector components [ as required notationally ] .
Both vectors and one- forms have four components but they have different
geometrical interpretation. Vectors are like arrows but one- forms can be
thought of as like three dimensional surfaces with the spacing between the
surfaces defining the magnitude of [ see Figure 3.1 ].